The world of Large Language Models (LLMs) is witnessing a quiet but fundamental revolution. While much of the industry focuses on adding more parameters, DeepSeek has taken a different route—reimagining the very geometry of how neural networks pass information.
Their latest breakthrough, Manifold-Constrained Hyper-Connections (mHC), effectively builds a "Topological Transformer." This new architecture not only solves the notorious instability problems of deep networks but is also beautifully compatible with the latest Google Transformer architectures (such as Titans and infinite-context models).
In this article, we’ll break down exactly what mHC is, why it matters, and dive deep into the fascinating mathematics behind it—specifically, how the Sinkhorn-Knopp algorithm allows us to "entropically project" residual connections onto the Birkhoff polytope.
The Bottleneck: Why Standard Transformers Get Unstable
To understand DeepSeek’s innovation, we first need to look at the flaw in current architectures.
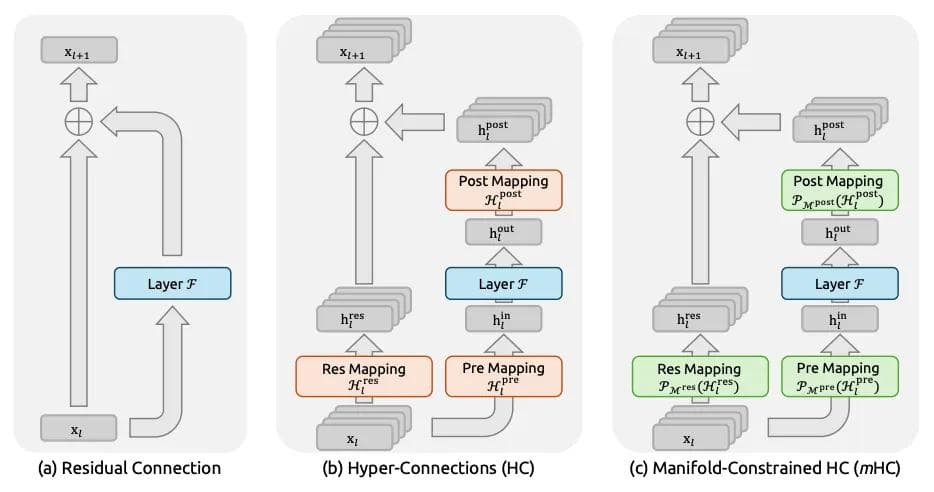
Modern Transformers (like GPT-4, Llama 3, or Gemini) rely heavily on Residual Connections. These are the "short circuits" that allow data to skip over processing layers. Mathematically, it looks like this:
This addition (+) creates a safe "highway" for information (gradients) to flow through the network without vanishing. This property is called Identity Mapping.
The Problem with Scaling
As models get wider and deeper, a single residual stream becomes a bottleneck. Researchers tried to fix this with Hyper-Connections (HC)—splitting the residual stream into multiple parallel "lanes" that mix together.
While this increases bandwidth, it breaks the safety of the highway. The signals start to explode or vanish, leading to training collapse. DeepSeek’s mHC fixes this by using geometry.
Enter Manifold-Constrained Hyper-Connections (mHC)
DeepSeek’s solution is elegant: allow the multiple lanes of Hyper-Connections to mix, but constrain that mixing to a very specific geometric shape (a manifold) that guarantees stability.
They force the connection matrices to live on the Birkhoff Polytope.
What is the Birkhoff Polytope?
Imagine a geometric shape existing in high-dimensional space. The Birkhoff Polytope is the set of all doubly stochastic matrices.
For a matrix to be "doubly stochastic," it must satisfy two simple rules:
- Every row sums to exactly 1.
- Every column sums to exactly 1.
When your residual connections are doubly stochastic, they preserve the total "energy" or magnitude of the signal as it flows through the network. The signal doesn't blow up (explode) and it doesn't fade away (vanish). It is perfectly conserved.
The Mathematics: Sinkhorn-Knopp and Entropic Projection
This is the core of DeepSeek's topological magic. The model produces a "raw" residual matrix (
) that is messy and unstable. We need to force this matrix onto the stable Birkhoff Polytope.
How do we move a messy matrix onto this perfect geometric shape efficiently during training? We use the Sinkhorn-Knopp Algorithm.
1. The Goal: Entropic Projection
We are looking for a new matrix P (on the polytope) that is as close as possible to our raw matrix H. In mathematics, "closeness" is often measured by entropy.
We want to solve an optimization problem: find the matrix P that minimizes the Kullback-Leibler (KL) divergence (relative entropy) from our original matrix H, subject to the constraints that rows and columns sum to 1.
2. The Algorithm: Sinkhorn-Knopp16
The Sinkhorn-Knopp algorithm is a remarkably simple iterative method to solve this complex projection. It works by alternating between normalizing rows and columns.
Let H be our raw, non-negative matrix.
We create two vectors, r (row scaling) and c (column scaling).
The Iteration:
- Normalize Rows: Divide every row by its sum so it equals 1.
- Normalize Columns: Divide every column of the result by its sum so it equals 1.
- Repeat: Keep doing this back and forth.
Mathematically, if we denote the matrix at step k as
The algorithm converges incredibly fast. After just a few iterations, the matrix $H$ transforms into a doubly stochastic matrix $P$ that lies perfectly on the Birkhoff Polytope.
Why "Entropic"?
The reason this is called "entropic projection" is that the Sinkhorn algorithm is actually solving the Entropic Optimal Transport problem. It finds the "cheapest" way to transport the mass from the rows to the columns while adding an entropy penalty (which encourages smoothness).
In the context of DeepSeek’s transformer, this ensures that the information flow remains smooth, stable, and distributed, rather than getting stuck in a few dominant neurons.
Compatibility with Google’s New Architecture
Why is this "beautifully compatible" with Google’s new Transformer designs (like the Titans architecture or Neural Memory)?
Google’s recent advancements focus on Long-Term Memory and Infinite Context.
- Titans use a "Neural Memory" module that learns to store facts over time.
- For these memory modules to work, they need a pristine signal from the deep past.
Standard transformers degrade the signal over thousands of layers (the "vanishing gradient" problem). By using DeepSeek’s mHC, the signal is topologically protected. The Birkhoff constraint ensures that the memory gradient can flow backward through thousands of layers without corruption.
It effectively creates a lossless fiber-optic cable (mHC) for Google’s massive data centers (Titans/Memory).
Key Benefits of Topological Transformers
- Unbreakable Stability: You can stack layers much deeper (100+ layers) without the model collapsing.
- Higher Bandwidth: Unlike standard residuals, mHC allows multiple streams of information to flow in parallel.
- Training Efficiency: Because the signal doesn't degrade, the model converges faster, saving millions in compute costs.
- Mathematical Elegance: It replaces "hacks" (like LayerNorm tuning) with principled geometry.
FAQ: DeepSeek mHC & Sinkhorn-Knopp
Q: Is the Sinkhorn-Knopp algorithm slow? A: No. It is highly parallelizable on GPUs. DeepSeek uses a version that requires only a few iterations to get "close enough" to the manifold, making it computationally cheap.
Q: Can I use this with existing models like Llama? A: Not directly. It requires changing the architecture of the residual blocks. However, future open-source models will likely adopt this topology.
Q: What is a "Topological" Transformer? A: "Topology" refers to properties that are preserved under deformation. By constraining the weights to the Birkhoff Polytope, the network preserves the "identity" property of the signal regardless of how deep the network gets.
Q: Does this replace Attention? A: No. mHC replaces the residual connections (the wiring between layers), not the Attention mechanism itself. It makes Attention more effective by giving it cleaner data.
Conclusion
DeepSeek’s Manifold-Constrained Hyper-Connections represent a shift from "engineering" to "geometry." By forcing the chaotic energy of a neural network to obey the strict laws of the Birkhoff Polytope, they have solved one of the oldest problems in Deep Learning: depth instability.
Using the Sinkhorn-Knopp algorithm, we can now project our networks into a stable mathematical space, paving the way for the next generation of Google-compatible, infinite-context AI models.
About the Author
Suraj - Writer Dock
Suraj Kumar is a writer, entrepreneur, and the CEO and founder of this website, sharing simple and practical insights on business, creativity, and personal growth. With experience building digital projects, they enjoy helping others learn, grow, and succeed online.
